Contents

Optimal Estimation Algorithms: Kalman and Particle Filters
An introduction to the Kalman and Particle Filters and their applications in fields such as Robotics and Reinforcement Learning.
Optimal Estimation Algorithms
Optimal Estimation Algorithms plays a really important role in our everyday life. Today, I will introduce you to two of them (Kalman and Particle Filters) using some practical examples.
Let’s imagine we are driving in a driverless car, and we are about to go through a long tunnel. In this example, our car makes use different sensors such as GPS estimation, accelerometers and cameras in order to keep track of its position in a map and of its interaction with other vehicles or pedestrian. Although, when travelling in a tunnel (especially in a really long one) our GPS signal becomes weaker because of interferences. Therefore, it might become more difficult for our car to estimate its position. What could we do in order to solve this problem?
One simple solution could be to use our accelerometer sensor data in combination with our weak GPS signal. In fact, taking a double integral of our acceleration we can be able to calculate our car position. Although, this simple measurement will contain some drift and will therefore not be totally accurate as our measurement errors will propagate through time (Figure 1). In order to solve this problem, we can use either a Kalman Filter or a Particle Filter.
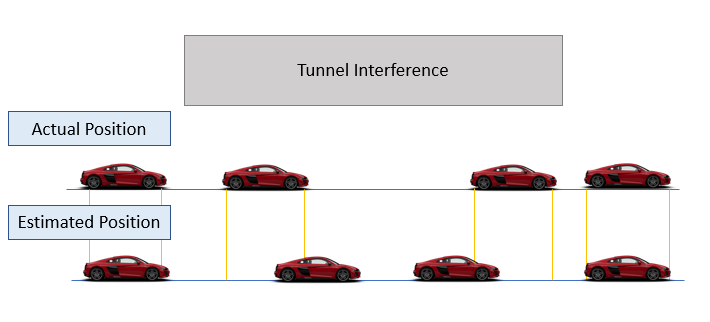
Figure 1: Autonomous car position estimation against time
Kalman Filter
Kalman Filters have common applications in Robotics (eg. SLAM Systems) and Reinforcement Learning. Kalman Filters can be used in Robotis in order to keep track of the movements of a swarm of robots in an environment and in Reinforcement Learning in order to keep track of different Software Agents.
A Kalman Filter is an iterative mathematical process which uses a set of equations and consecutive data inputs in order to estimate the true position, velocity, etc… of an object when the measured values contain uncertainties or errors. [1]
Kalman FIlters can, therefore, be simplistically compared to Machine Learning models. They take some input data, perform some calculations in order to make an estimate, calculate its estimation error and iteratively repeat this process in order to reduce the final loss. The iterative process performed by a Kalmar Filter can be summarised in 3 main steps:
- Kalman Gain Calculation: is computed by using the error in the input data and in the estimation.
- Current Estimate Calculation: is computed using the raw input data, our previous estimate and the Kalman Gain.
- Estimation Error Calculation: is finally calculated using the Kalman Gain and our Current Estimate.
This process is briefly summarised in Figure 2.
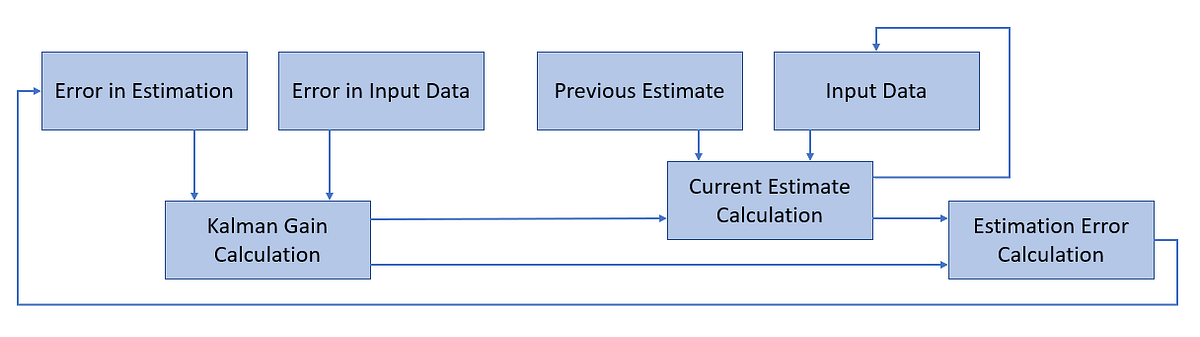
Figure 2: Kalman Filter WorkFlow (Adapted from [1])
There exist different varieties of Kalman Filters, some examples are: linear Kalmar Filter, Extended Kalman filter and Unscented Kalman Filter. If you are interested in a more detailed mathematical explanation of Kalman Filters, this tutorial by MIT Tony Lacey is a great place where to start [2].
One of the main problems of Kalman Filters is that they can only be used in order to model situations which can be described in terms of Gaussian Noises. Although, many non-gaussian processes can be either approximated in gaussian terms or transformed in Gaussian distributions through some form of transformation (eg. logarithmic, square root, etc..).
In order to overcome this type of limitation, an alternative method can be used: Particle Filters.
Particle Filter
Particle FIlters can be used in order to solve non-gaussian noises problems, but are generally more computationally expensive than Kalman Filters. That’s because Particle Filters uses simulation methods instead of analytical equations in order to solve estimation tasks.
Particle Filters are commonly used in:
- Financial Markets Analysis (especially in stochastic processes analysis)
- Reinforcement Learning
- Robots Localization (eg. direct global policy search)
Particle Filters are based on Monte Carlo Methods and manage to handle not gaussian problems by discretizing the original data into particles (each of them representing a different state). The greater the number of particles and the better our Particle Filter would be able to handle any possible type of distribution.
Like Kalman Filters, Particle Filters also make use of an iterative process in order to produce its estimations. Each iteration can be broken down into three main steps [3]:
- Take multiple samples (particles) from an original distribution.
- Weight all the sampled particles in order of importance (the more particles fall in a given interval and the higher is their probability density).
- Resampling by replacing more unlikely particles with more likely ones (like in evolutionary algorithms, only the fittest elements of a population survive).
This process is summed up in Figure 3. As we can see from the figure below, in this example, our Particle Filter is able just after one iteration to understand in which range is more likely to be our object. Repeating iteratively this process, our filter would then be able to restrict even more its dispersion range.
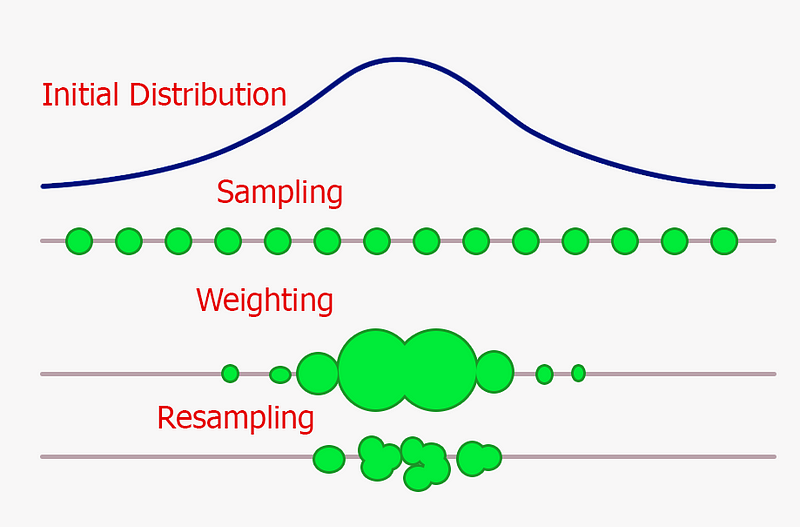
Figure 3: Single Particle Filter Iteration
If you are interested in implementing optimal estimation algorithms in Python, the FilterPy or Pyro libraries are two great solutions. In particular, Pyro is a universal probabilistic programming language developed by Uber which can be used for various Bayesian analysis using PyTorch as backend.
I hope you enjoyed this article, thank you for reading!
Bibliography
[1] Special Topics — The Kalman Filter (2 of 55) Flowchart of a Simple Example (Single Measured Value), Michel van Biezen. Accessed at: https://www.youtube.com/watch?v=CaCcOwJPytQ
[2] Chapter 11. Tutorial: The Kalman Filter, Tony Lacey. Accessed at: http://web.mit.edu/kirtley/kirtley/binlustuff/literature/control/Kalman%20filter.pdf
[3] Short Introduction to Particle Filters and Monte Carlo Localization, Cyrill Stachniss. Accessed at: http://ais.informatik.uni-freiburg.de/teaching/ws12/mapping/pdf/slam09-particle-filter-4.pdf
Contacts
If you want to keep updated with my latest articles and projects follow me on Medium and subscribe to my mailing list. These are some of my contacts details:
