Contents
 (Source: https://www.thegreatcourses.com/)
(Source: https://www.thegreatcourses.com/)
Game Theory in Artificial Intelligence
An Introduction to Game Theory and how it can be applied to the different ambit of Artificial Intelligence.
Introduction
Game Theory is a branch of mathematics used to model the strategic interaction between different players in a context with predefined rules and outcomes.
Game Theory can be applied in different ambit of Artificial Intelligence:
- Multi-agent AI systems.
- Imitation and Reinforcement Learning.
- Adversary training in Generative Adversarial Networks (GANs).
Game Theory can also be used to describe many situations in our daily life and Machine Learning models (Figure 1).
For example, a Classification algorithm such as SVM (Support Vector Machines) can be explained in terms of a two-player game in which one player is challenging the other to find the best hyper-plane giving him the most difficult points to classify. The game will then converge to a solution which will be a trade-off between the strategic abilities of the two players (eg. how well the fist player was challenging the second one to classify difficult data points and how good was the second player to identify the best decision boundary).
Figure 1: Game Theory Applications [1]
Game Theory
Game Theory can be divided into 5 main types of games:
- Cooperative vs Non-Cooperative Games: In cooperative games, participants can establish alliances in order to maximise their chances to win the game (eg. negotiations). In non-cooperative games, participants can’t instead form alliances (eg. wars).
- Symmetric vs Asymmetric Games: In a symmetric game all the participants have the same goals and just their strategies implemented in order to achieve them will determine who wins the game (eg. chess). In asymmetric games instead, the participants have different or conflicting goals.
- Perfect vs Imperfect Information Games: In Perfect Information games all the players can see the other players moves (eg. chess). Instead, in Imperfect Information games, the other players’ moves are hidden (eg. card games).
- Simultaneous vs Sequential Games: In Simultaneous games, the different players can take actions concurrently. Instead in Sequential games, each player is aware of the other players’ previous actions (eg. board games).
- Zero-Sum vs Non-Zero Sum Games: In Zero Sum games, if a player gains something that causes a loss to the other players. In Non-Zero Sum games, instead, multiple players can take benefit of the gains of another player.
Different aspects of Game Theory are commonly used in Artificial Intelligence, I will now introduce you to the Nash Equilibrium, Inverse Game Theory and give you some practical examples.
If you are interested in implementing Game Theory Algorithms in Python, the Nashpy library is a good place where to start.
Nash Equilibrium
The Nash Equilibrium is a condition in which all the players involved in the game agree that there is no best solution to the game than the actual situation they are in at this point. None of the players would have an advantage in changing their current strategy (based on the decisions made by the other players).
Following our example of before, an example of Nash Equilibrium can be when the SVM classifier agrees on which hyper-plane to use classify our data.
One of the most common examples used to explain Nash Equilibrium is the Prisoner’s Dilemma. Let’s imagine two criminals get arrested and they are held in confinement without having any possibility to communicate with each other (Figure 2).
- If any of the two prisoners will confess the other committed a crime, the first one will be set free while the other will spend 10 years in prison.
- If neither of them confesses they spend just one year in prison for each.
- If they both confess, they instead both spend 5 years in prison.

Figure 2: Payoff Matrix [2]
In this case, the Nash Equilibrium is reached when both criminals betray each other.
An easy way to find out if a game has reached a Nash Equilibrium can be to reveal your strategy to your opponents. If after your revelation, none of them changes their strategy, the Nash Equilibrium is demonstrated.
Unfortunately, a Nash Equilibrium is easier to be achieved in Symmetric than Asymmetric games. Asymmetric games are in fact the most common in real-world applications and Artificial Intelligence.
Inverse Game Theory
Game Theory aims to understand the dynamics of a game to optimise the possible outcome of its players. Inverse Game Theory instead aims to design a game based on the players’ strategies and aims. Inverse Game Theory plays an important role in designing AI Agents environments.
Practical Examples
Adversary training in Generative Adversarial Networks (GANs)
GANs consists of two different models: a generative model and a discriminative model (Figure 3).
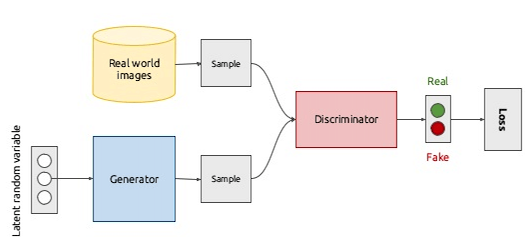
Figure 3: GAN Architecture [3]
Generative models take as input some features, examine their distributions and try to understand how they have been produced. Some examples of generative models are Hidden Markov Models (HMMs) and Restricted Boltzmann Machines (RBMs).
Discriminative Models instead take the input features to predict to which class our sample might belong. Support Vector Machines (SVM) is an example of a discriminative model.
In GANs, the generative model uses the input features to create new samples which aim to resemble quite closely the main characteristics of the original samples. The newly generated samples are then passed with the original ones to the discriminative model which has to recognise which samples are genuine and which ones are fake [4].
An example application of GANs can be to generate images and then distinguish between real and fake ones (Figure 4).

Figure 4: Images generated by NVIDIA GAN! [5]
This process resembles quite closely the dynamics of a game. In this game, our players (the two models) are challenging each other. The first one creates fake samples to confuse the other, while the second player tries to get better and better at identifying the right samples.
This game is then repeated iteratively and in each iteration, the learning parameters are updated in order to reduce the overall loss.
This process will keep going on until Nash Equilibrium is reached (the two models become proficient at performing their tasks and they are not able to improve anymore).
Multi-Agents Reinforcement Learning (MARL)
Reinforcement Learning (RL) aims to make an agent (our “model”) learn through the interaction with an environment (this can be either virtual or real).
RL was firstly developed to adhere to Markov Decision Processes. In this ambit, an agent is placed in a stochastic stationary environment and tries to learn a policy through a reward/punishment mechanism. In this scenario, it is proved the agent will converge to a satisfactory policy.
However, if multiple agents are placed in the same environment, this condition is no longer true. In fact, before the learning of the agent was only dependent on the interaction between the agent and the environment, now it is also dependent on the interaction between agents (Figure 5).
Let’s imagine we are trying to improve the traffic flow in a city using a group of AI-powered Self-Driving Cars. On their own, each of the cars can perfectly interact with the external environment but things can get more complicated if we want to make the cars think as a group. For example, a car might get in conflict with another one because for both of them is most convenient to follow a certain route.
This situation can be easily modelled using Game Theory. In this case, our cars would represent the different players and the Nash Equilibrium the equilibrium point between the collaboration between the different cars.

Figure 5: Multi-Agents Reinforcement Learning Tennis [6]
Modelling systems with a large number of agents can become a really difficult task. That’s because, increasing the number of agents, makes increase exponentially the number of possible ways the different agents interact with each other.
In these cases, modelling Multi-Agents Reinforcement Learning Models with Mean Field Scenarios (MFS) might be the best solution. Mean Field Scenarios can, in fact, reduce the complexity of MARL models by making the assumption a priori that all agents have similar reward functions.
Bibliography
[1] Game Theory & Optimal Decisions. Accessed at: http://euler.fd.cvut.cz/predmety/game_theory/
[2] Quantum Probabilistic Models Revisited: The Case of Disjunction Effects in Cognition. Catarina Moreira, et al. Researchgate. Accessed at: https://www.researchgate.net/publication/304577699Quantum_Probabilistic_Models_Revisited The_Case_of_Disjunction_Effects_in_ Cognition/figures?lo=1
[3] GAN Deep Learning Architectures — review, Sigmoidal. Accessed at: https://sigmoidal.io/beginners-review-of-gan-architectures/
[4] Overview: Generative Adversarial Networks — When Deep Learning Meets Game Theory. AHMED HANI IBRAHIM. Accessed at: https://ahmedhanibrahim.wordpress.com/2017/01/17/generative-adversarial-networks-when-deep-learning-meets-game-theory/comment-page-1/
[5] Nvidia AI Generates Fake Faces Based On Real Celebs - Geek.com. Accessed at: https://www.geek.com/tech/nvidia-ai-generates-fake-faces-based-on-real-celebs-1721216/
[6] David Brown, Tennis Environment — Multi-Agent Reinforcement Learning. Accessed at: https://github.com/david-wb/marl
Contacts
If you want to keep updated with my latest articles and projects follow me on Medium and subscribe to my mailing list. These are some of my contacts details:
