Contents
Online Learning: Recursive Least Squares and Online PCA
A practical introduction on how to create online Machine Learning models able to train one data point at the time processing streaming data
Online Learning
Online Learning, is a subset of Machine Learning which emphasizes the fact that data generated from environments can change over time.
In fact, traditional Machine Learning models are instead considered to be static: once a model is trained on a set of data it’s parameters don’t change any more. Although, an environment and it’s generated data might change over time making, therefore, our pre-trained model not reliable anymore.
One simple solution which is commonly used by companies in order to solve these problems is to retrain and deploy an updated version of the Machine Learning model automatically once the performance starts decreasing.
Although, using this approach would then lead to having a model which periodically performs worse than it’s expected standards [1]. Online Learning can then be used in order to provide a definitive answer to this problem.
If you are interested in implementing Online Learning Algorithms in Python, the Creme library is a good place where to start.
All the code used in this article is available (and more!) is available on my GitHub Profile.
Recursive Least Squares
Introduction
Recursive Least Squares (RLS) is a common technique used in order to study real-time data. RLS can, therefore, be considered as the recursive equivalent of the standard least-squares algorithm.
In Recursive Least Squares a single new data point is analysed each algorithm iteration in order to improve the estimation of our model parameters (in this case the aim is not to minimize the overall mean squared error like for example in Least Mean Squared).
Compared to other regression techniques, RLS usually tends to much faster convergence but higher computational costs.
Two important observations about this algorithm are:
- A user-defined parameter called Lambda (λ) is used in order to define how much weight to give to past input data (older inputs have less predictive weight than more recent ones). The smaller the value of λ and the lower will be the importance of past input values.
- In order to avoid computing matrix inversion at each iteration step (which can be computationally costly), we can instead apply the Matrix Inversion Lemma.
If you are interested in the implementation details of this algorithm, the mathematical derivation is available in “Lectures on Dynamic Systems and Control” by MIT Open Courseware [2].
Demonstration
In order to test this algorithm, we are going to use in this article the
Daily Demand Forecasting Orders Data Set from the UCI Machine Learning Repository.
First of all, we need to import the required dependencies and divide our dataset into features and labels. Our objective in this exercise will be to predict the total number of orders given our input features (Figure 1).
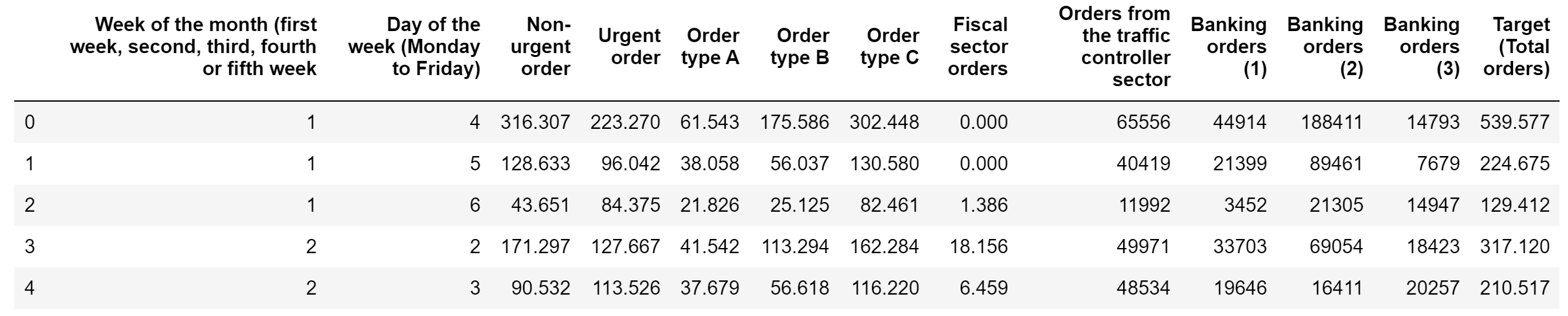
Figure 1: Daily Demand Forecasting Orders Data Set
We can now create our own implementation of the Recursive Least Squares algorithm and check our residual error.
Residual Error: 0.851
As shown by the low Residual Error, our algorithm seemed to have successfully converged towards a relatively reliable solution. This can be additionally confirmed by comparing our results using instead a Mini Batch Gradient Descent Algorithm for the same task (Figure 2).

Figure 2: Recursive Least Squares vs Mini Batch Gradient Descent
Plotting the actual time series values against the Recursive Least Squares estimated ones we can ulteriorly confirm the reliability of our model for this simple problem (Figure 3).

Figure 3: Total Orders Estimation Comparison
Finally, by creating a simple function we can compare the overall Residual Error of our model against some common Scikit-Learn models to compare performances. As shown by the results below, just the Gaussian Process Regressor seemed to perform better than Recursive Least Squares.
SGDRegressor Residual Error: 83.905
DecisionTreeRegressor Residual Error: 84.853
GaussianProcessRegressor Residual Error: 0.0
KNeighborsRegressor Residual Error: 2.296
BayesianRidge Residual Error: 84.853
MLPRegressor Residual Error: 84.661
Online Principal Component Analysis
When working with datasets with a considerable amount of features, Online PCA could certainly be considered a good technique to implement in order to try to reduce the dimensionality of our problem, speed up at the same time the execution speed and bound our error within a user-defined limit. Online Principle Component Analysis tries to apply the same basic concepts of PCA in an online context, by creating its estimates taking as input one data point at the time.
One of the main parameters of this algorithm is Epsilon (ε). Epsilon is what we can tolerate with respect to the given data (the error). The algorithm will then return an l dimensional representation (O(k×poly(1/ε))) slightly higher than the desired k dimensional representation (but still lower than the original d dimensional representation).
Using a small ε, we force our algorithm to not tolerate much error and therefore this would lead to a high-value for l. Using instead a high ε, we allow our algorithm to tolerate high errors and enable to use a low-value for l. Following Boutsidis et al. [3] implementation, ε can be represented by any value between 0 and 1/15. In this way, Online PCA allows us to create a trade-off between desired dimensionality and maximum allowed error.
Some of the additional advantages of using this algorithm are:
- Online PCA can enable us to make inferences in lower dimensions, denoise our input data and achieve important computational savings (especially when working with datasets belonging to the Big Data regime).
- Using optimized versions of Online PCA, it is possible to avoid calculating all the eigenvalues and eigenvectors for the whole covariance matrix (which can be quite big) and compute instead just the first N eigenvalues and eigenvectors which we are interested in.
In case you are interested in implementing Online PCA, Boutsidis et al. [3] publication is a great place where to start.
I hope you enjoyed this article, thank you for reading!
Bibliography
[1] What is Online Machine Learning? Max Pagels, FOURKIND. Accessed at: https://medium.com/value-stream-design/online-machine-learning-515556ff72c5
[2] Lectures on Dynamic Systems and Control. Mohammed Dahleh et al, MIT Open Courseware. Accessed at: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-241j-dynamic-systems-and-control-spring-2011/readings/MIT6_241JS11_chap02.pdf
[3] Boutsidis, C, Garber D, Karnin ZS and Liberty, E. Online principal components analysis, Proceedings of the twenty-sixth annual ACM-SIAM symposium on Discrete algorithms, SODA-15: 887–901, 2015.
Contacts
If you want to keep updated with my latest articles and projects follow me on Medium and subscribe to my mailing list. These are some of my contacts details:
